Matrix Multiplication
Two matrices A and B are said to be conformable for multiplication if the number of columns of the first matrix A is equal to the number of rows of the second matrix B.
The product matrix AB is acquired by multiplying every row of matrix A with the corresponding elements of every column of matrix B element-wise and add the results. This procedure is known as row-by-column multiplication rule.
Let A be a matrix of order m×n and B be a matrix of order n×p then the product matrix AB will be of order m×p.
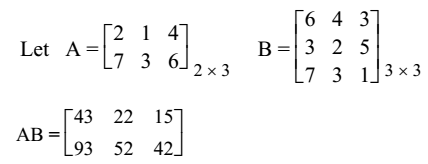
- (2) (6) + (1) (3) + (4) (7) = 43
- (2) (4) + (1) (2) + (4) (3) = 22
- (2) (3) + (1) (5) + (4) (1) = 15
- (7) (6) + (3) (3) + (6) (7) = 93
- (7) (4) + (3) (2) + (6) (3) = 52
- (7) (3) + (3) (5) + (6) (1) = 42
Order of AB is 2 ×3, which is the number of rows of first matrix A by the number of columns of the second matrix B.
If AB = AC, it is not necessarily true that B = C. The equal matrices in the identity cannot be cancelled as in algebra.
AB = O does not necessarily imply A = O or B = O.
If A is a square matrix then A.A is also a square matrix of the same order. AA is denoted by A2.
If I is a unit matrix, then I = I2 = I3 = In.
