Maximum and Minimum Values
Some of the most important applications of differential calculus are optimization problems, in which you are required to find the optimal (best) way of doing something. These problems can be reduced to finding the maximum or minimum values of a function. Many practical problems require to minimize a cost or maximize an area.
The gradient (rate of change) of the curve changes from positive between O and P to negative between P and Q and positive again between Q and R. At point P, the gradient is zero and as x increases, the gradient (slope) of the curve changes from positive just before P to negative just after. Such a point is called a maximum point and appears as the crest of a wave.
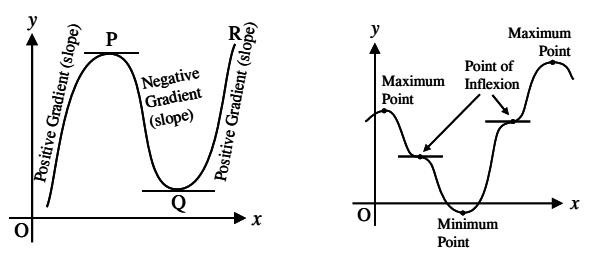
At point Q, the gradient is also zero and as x increases the gradient of the curve changes from negative just before Q to positive just after. Such a point is called a minimum point and appears as the bottom of a valley.
Points such as P and Q are given the general name, turning points.
It is possible to have a turning point, the gradient on either side of which is the same. Such a point is called a point of inflection.
Absolute and Local
A function f has an absolute maximum at c if f(c) ≥ f(x) for all x in D, where D is the domain of f. The number f(c) is called maximum value of f on D. Similarly f has an absolute minimum at c if f(c) ≤ f(x) for all x in D and the number f(c) is called the minimum value of f on D. The maximum and minimum values of f are called extreme values of f.
A function f has a local maximum (or relative maximum) at c if there is an open interval I containing c such that f(c) ≥ f(x) for all x in I. Similarly, f has a local minimum at c if there is an open interval I containing c such that f(c) ≤ f(x) for all x in I.
Fermat’s Theorem
If f has a local extremum (maximum or minimum) at c and if f′(c) exists then f′(c) = 0. However, even when f′(c) = 0 there need not be a maximum or minimum at c.
Critical Points
A critical number of a function f is a number c in the domain of f such that either f′(c) = 0 or f′(c) does not exist. Stationary points are critical numbers c in the domain of f, for which f′(c) = 0.
Second Derivative Test
Suppose f is continuous on an open interval that contains c.
- If f′(c) = 0 and f′′(c) > 0, then f has a local minimum at c.
- If f′(c) = 0 and f′′(c) < 0, then f has a local maximum at c.