Parametric Form of Circle
Consider a circle with radius rand centre at the origin. Let P(x, y) be any point on the circle. Assume that OP makes an angle θwith the positive direction of x-axis. Draw the perpendicular PM to the x-axis.
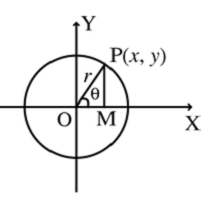
cos θ = x/r
sin θ = y/r
x and y are the co-ordinates of any point on the circle. These two co-ordinates depend on θ. The value of r is fixed.
The equations x = r cosθ, y = r sinθ are called the parametric equations of the circle x2 + y2 = r2.
θ is called the parameter and 0 ≤ θ ≤2π.