Maths Chapter-03: Trigonometric Functions
Exercise 3.1
Q.1: Calculate the radian measurement of the given degree measurement:
(i). \(25\;^{\circ}\)
(ii). \(240\;^{\circ}\)
(iii). \(-47\;^{\circ} \; 30?\)
(iv). \(520\;^{\circ}\)
Sol:
(i). \(25\;^{\circ}\)
As we know that, \(180\;^{\circ}\) = ? radian
Therefore, \(25\;^{\circ}\) = \(\frac{\pi }{180} \times 25\) radian = \(\frac{5\pi }{36}\) radian
Hence, \(25\;^{\circ}\) = \(\frac{5\pi }{36}\) radian
(ii). \(240\;^{\circ}\)
As we know that \(180\;^{\circ}\) = ? radian
Therefore, \(240\;^{\circ}\) = \(\frac{\pi }{180} \times 240\) radian = \(\frac{4\pi }{3}\) radian
Hence, \(240\;^{\circ}\) = \(\frac{4\pi }{3}\) radian
(iii). \(-47\;^{\circ} \; 30?\)
= \(-47\frac{1}{2}\)
= \(\frac{-95}{2}\) degree
As we know that, \(180\;^{\circ}\) = ? radian
Therefore, \(\frac{-95}{2}\) degree = \(\frac{\pi }{180}\times \frac{-95}{2}\) radian = \(\frac{-19 }{36\; \times \;2}\pi\) radian = \(\frac{-19 }{72}\pi\)
Hence, \(-47\;^{\circ} \; 30?\) = \(\frac{-19 }{72}\pi\)
(iv). \(520\;^{\circ}\)
As we know that, \(180\;^{\circ}\) = n radian
Therefore, \(520\;^{\circ}\) = \(\frac{\pi }{180} \times 520\) radian = \(\frac{26\pi }{9}\) radian
Hence, \(520\;^{\circ}\) = \(\frac{26\pi }{9}\) radian
Q.2: Calculate the degree measurement of the given degree measurement: [Use ? = \(\frac{22}{7}\)]
(i) \(\frac{11}{16}\)
(ii) -4
(iii) \(\frac{5\pi }{3}\)
(iv) \(\frac{7\pi }{6}\)
Sol:
(i). \(\frac{11}{16}\):
As we know, that ? Radian = 180°
Therefore, \(\frac{11}{16}\) radian = \(\frac{180}{\pi }\times \frac{11}{16}\) degree
= \(\frac{45\times 11}{\pi \times 4 }\) degree
= \(\frac{45 \times 11 \times 7}{22 \times 4 }\) degree
= \(\frac{315}{8}\) degree
= \(39\;\frac{3}{8}\) degree
= \(39\;^{\circ} \;+ \; \frac{3\times 60}{8}\) minute [\(1^{\circ}\) = 60’]
= \(39^{\circ} \;+ \; 22? \;+ \;\frac{1}{2}\) minute
= \(39^{\circ} \;+ \; 22? \;+ \;30”\) [1’ = 60’’]
(ii). -4:
As we know, that ? Radian = 180°
Therefore, -4 radian = \(\frac{180}{\pi } \times (-4)\) degree
= \(\frac{180 \times 7(-4)}{22}\) degree
= \(\frac{-2520}{11}\) degree
= \(-229\frac{1}{11}\) degree
= \(-229^{\circ} \; + \; \frac{1\times 60}{11}\) minutes [\(1^{\circ}\) = 60’]
= \(-229^{\circ} \; +\; 5? +\;\frac{5}{11}\)
= \(-229^{\circ} \; +\; 5? +\;27”\) [1’ = 60’’]
(iii). \(\frac{5\pi }{3}\)
As we know, that ? Radian = 180°
Therefore, \(\frac{5\pi}{3}\) radian = \(\frac{180}{\pi }\times \frac{5\pi}{3}\) degree
= \(300^{\circ}\)
(iv). \(\frac{7\pi }{6}\)
As we know, that ? Radian = 180°
Therefore, \(\frac{7\pi}{6}\) radian = \(\frac{180}{\pi }\times \frac{7\pi }{6}\)
= \(210^{\circ}\)
Q.3: In a minute, wheel makes 360 revolutions. Through how many radians does it turn in 1 second?
Answer:
No. of revolutions made in a minute = 360 revolutions
Therefore, no. of revolutions made in a second = \(\frac{360}{60}\) = 6
In one revolution, the wheel rotates an angle of 2? radian.
Therefore, in 6 revolutions, it will turn an angle of 12? radian.
Q.4: Calculate the degree measurement of the angle subtended at the centre of a circle of radius 100 m by an arc of length 22 m.
[Use ? = \(\frac{22}{7}\)]
Answer:
As we know,
In a circle of radius r unit, if an arc of length l unit subtends an angle ? radian at the centre, then, \(\theta = \frac{l}{r}\)
Given:
r = 100 m and L = 22 m
We have,
\(\theta = \frac{22}{100}\) radian
= \(\frac{180}{\pi }\times \frac{22}{100}\) degree
= \(\frac{180 \;\times \;7 \;\times \;22}{22 \; \times 100 }\) degree
= \(\frac{126}{10 }\) degree
= \(12\frac{3}{5}\) degree
= \(12^{\circ} \; 36?\) [\(1^{\circ}\) = 60’]
Therefore, the req angle is \(12^{\circ} \; 36?\)
Q.5: In a circle of diameter 40 m, the length of the chord 20 m. Find the length of minor arc of chord.
Answer:
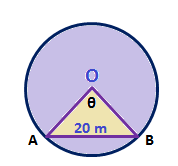
Diameter of circle = 40 m
Radius of circle = \(\frac{40}{20}\) m = 20 m
Let XY be the chord (length = 20 m) of the circle.
In \(\Delta OXY\), OX = OY = radius of the circle = 20 m
XY = 20 m
Therefore,
\(\Delta OXY\) is an equilateral triangle.
\(\theta \;= \;60^{\circ}\) = \(\frac{\pi }{3}\) radian
As we know,
In a circle of radius r unit, if an arc of length l unit subtends an angle ? radian at the centre, then, ? = \(\frac{l}{r}\)
\(\frac{\pi }{3}\) = \(\frac{arc\;(AB\;)}{20}\)
\(\frac{arc\;(AB\;)}{20}\) = \(\frac{20\pi }{3}\) m
The length of the minor arc of the chord is \(\frac{20\pi }{3}\) m.
Q.6: In two circles, arcs which has same length subtended at an angle of \(60^{\circ}\) and \(75^{\circ}\) at the center. Calculate the ratio of their radii.
Sol:
Let, the radii of two circles be \(r_{1}\) and \(r_{2}\).
Let, an arc of length l subtend an angle of \(60^{\circ}\) at the center of the circle of radius \(r_{1}\), while let an arc of length l subtend an angle of \(75^{\circ}\) at the center of the circle of radius \(r_{2}\).
\(\\60^{\circ}\) = \(\frac{\pi }{3}\) radian
\(75^{\circ}\) = \(\frac{5\pi }{12}\) radian
In a circle of radius r unit, if an arc of length l unit subtends an angle ? then:
? = \(\frac{l}{r}\)
l = r ?
l = \(\frac{r_{1}\;\pi }{3}\)
l = \(\frac{r_{2}\;5\pi }{12}\)
\(\frac{r_{1}\;\pi }{3}\) = \(\frac{r_{2}\;5\pi }{12}\)
\(r_{1}\) = \(\frac{r_{2}5}{4}\)
\(\frac{r_{1}}{r_{2}}\) = \(\frac{5}{4}\)
Therefore, the ratio of radii is 5: 4
Q.7: Calculate the angle in radian through which a pendulum swings if the length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm
Sol:
As we know that, in a circle of radius ‘r’ unit, if an arc of length ‘l’ unit subtends an angle \(\theta\) radian at the center, then:
\(\theta = \frac{l}{r}\\\)
Here, r = 75 cm
(i). 10 cm:
\(\theta\) = \(\frac{10}{75}\) radian = \(\frac{2}{15}\) radian
(ii). 15 cm:
\(\theta\) = \(\frac{15}{75}\) radian = \(\frac{1}{5}\) radian
(iii). 21 cm:
\(\theta\) = \(\frac{21}{75}\) radian = \(\frac{7}{25}\) radian
Exercise 3.2
Q.1: Calculate the values of five trigonometric func. if \(\cos y\) = \(-\frac{1}{2}\) and y lies in 3rd quadrant.
Sol:
(i) sec y :
Since, cos y = \(\frac{1}{2}\)
Therefore, sec y = \(\frac{1}{\cos y}\) = \(\frac{1}{\left (-\frac{1}{2} \right )}\)
Hence, sec y = -2
(ii) sin y :
Since, \(\sin ^{2}y \;+ \;\cos ^{2}y \;= \;1\)
Therefore, \(\sin ^{2}y \;= \;1 \;- \;\cos ^{2}y\)
\(\Rightarrow\) \(\sin ^{2}y \;= \;1 \;- \;\left (-\frac{1}{2} \right )^{2}\)
\(\Rightarrow\) \(\sin ^{2}y \;= \;1 \;- \;\frac{1}{4}\)
\(\Rightarrow\) \(\sin ^{2}y \;= \;\frac{3}{4}\)
\(\Rightarrow\) \(\sin y \;= \;\pm \frac{\sqrt{3}}{2}\)
Since, y lies in the third quadrant, the value of sin y will be negative.
Therefore, sin y = \(\frac{\sqrt{3}}{2}\)
(iii) cosec y = \(\frac{1}{\sin y}\) = \(\frac{1}{\left (-\frac{\sqrt{3}}{2} \right )}\) = \(-\frac{2}{\sqrt{3}}\)
Therefore, cosec y = \(-\frac{2}{\sqrt{3}}\)
(iv) tan y = \(\frac{\sin y}{\cos y}\) = \(\tan y=\frac{\left (-\frac{\sqrt{3}}{2} \right )}{\left (-\frac{1}{2} \right )}\) = \(\sqrt{3}\)
Therefore, tan y = \(\sqrt{3}\)
(v) cot y = \(\frac{1}{\tan y}\) = \(\frac{1}{\sqrt{3}}\)
Therefore, cot y = \(\frac{1}{\sqrt{3}}\)
Q.2: Calculate the other five trigonometric function if we are given the values for sin y = \(\frac{3}{5}\), where y lies in second quadrant.
Sol:
sin y = \(\frac{3}{5}\)
Therefore, cosec y = \(\frac{1}{Sin\; y}\) = \(\frac{1}{\frac{3}{5}} = \frac{5}{3}\)
Since, \(sin^{2}\;y \; + \; cos^{2}\;y = 1\)
\(\Rightarrow\) \( cos^{2} y = 1 – sin^{2} y\)
\(\Rightarrow\) \(cos^{2} y = 1 – \left ( \frac{3}{5} \right )^{2}\)
\(\Rightarrow\) \(cos^{2} y = 1 – \frac{9}{25}\)
\(\Rightarrow\) \(cos^{2} y = \frac{16}{25}\)
\(\Rightarrow\) cos y = \(\pm \frac{4}{5}\)
Since, y lies in the 2nd quadrant, the value of cos y will be negative,
Therefore, cos y = – \(\frac{4}{5}\)
\(\Rightarrow\) sec y = \(\frac{1}{cos \; y} = \frac{1}{\left (- \frac{4}{5} \right )} =\; – \frac{5}{4}\)
\(\Rightarrow\) tan y = \(\frac{sin \; y}{cos \; y} = \frac{\left (\frac{3}{5} \right ) }{\left (-\frac{4}{5} \right ) } = \;- \frac{3}{4}\)
\(\Rightarrow\) cot y = \(\frac{1}{tan \; y} =\;- \frac{4}{3}\)
Q.3: Find the values of other five trigonometric functions if \(cot \; y = \frac{3}{4}\), where y lies in the third quadrant.
Sol:
cot y = \(\frac{3}{4}\)
Since, tan y = \(\frac{1}{cot \; y}=\frac{1}{\frac{3}{4}}=\frac{4}{3}\)
Since, \(1 + tan^{2}y = sec^{2}y\)
\(\Rightarrow\) \(1 + \left ( \frac{4}{3} \right )^{2} = sec^{2}y\)
\(\Rightarrow\) \(1 + \frac{16}{9} = sec^{2}y\)
\(\Rightarrow\) \(\frac{25}{9} = sec^{2}y\)
\(\Rightarrow\) sec y = \(\pm \frac{5}{3}\)
Since, y lies in the 3rd quadrant, the value of sec y will be negative.
Therefore, sec y = \(\;- \frac{5}{3}\)
cos y = \(\frac{1}{sec \; y} = \frac{1}{\left (- \frac{5}{3} \right )} = – \frac{3}{5}\)
Since, tan y = \(\frac{sin \; y}{cos \; y}\)
\(\Rightarrow\) \( \frac{4}{3} = \frac{sin \; y}{\left (- \frac{3}{5} \right )}\)
\(\Rightarrow \) sin y = \(\left (\frac{4}{3} \right ) \times \left (- \frac{3}{5} \right ) = -\frac{4}{5}\)
\(\Rightarrow\) cosec y = \(\frac{1}{sin \; y} = -\frac{5}{4}\)
Q.4: Find the values of other five trigonometric if \(sec \; y = \frac{13}{5}\), where y lies in the fourth quadrant.
Sol:
sec y = \(\frac{13}{5}\)
cos y = \(\frac{1}{sec \; y} = \frac{1}{\left (\frac{13}{5}\right )} = \frac{5}{13}\)
Since, \(sin^{2}y + cos^{2}y = 1\)
\(\Rightarrow\) \(sin^{2}y = 1 – cos^{2}y\)
\(\Rightarrow\) \(sin^{2}y = 1 – \left ( \frac{5}{13} \right )^{2}\)
\(\Rightarrow\) \(sin^{2}y = 1 – \frac{25}{169} = \frac{144}{169}\)
\(\Rightarrow\) sin y = \(\pm \frac{12}{13}\)
Since, y lies in the 4th quadrant, the value of sin y will be negative.
Therefore, sin y = \(– \frac{12}{13}\)
\(\Rightarrow\) cosec y = \(\frac{1}{sin \; y} = \frac{1}{\left (- \frac{12}{13} \right )} = \;- \frac{13}{12}\)
\(\Rightarrow\) tan y = \(\frac{sin \; y}{cos \; y} = \frac{\left (- \frac{12}{13} \right )}{\left (\frac{5}{13} \right )} =\; -\frac{12}{5}\)
\(\Rightarrow\) cot y = \(\frac{1}{tan \; y} = \frac{1}{\left ( -\frac{12}{5} \right )} = \;-\frac{5}{12}\)
Q.5: Find the values of other five trigonometric function if tan y = \(– \frac{5}{12}\) and y lies in second quadrant.
Sol:
tan y = \(-\frac{5}{12}\) [Given]
And, cot y = \(\frac{1}{tan \; y} = \frac{1}{ \left (- \frac{5}{12} \right )} = – \frac{12}{5}\)
Since, \(1 + tan^{2} y = sec^{2} y\)
Therefore, \(1 + \left ( – \frac{5}{12} \right )^{2} = sec^{2} y\)
\(\Rightarrow\) \(sec^{2} y = 1 + \left ( \frac{25}{144} \right )\)
\(\Rightarrow \) \(sec^{2} y = \frac{169}{144}\)
\(\Rightarrow\) sec y = \(\pm \frac{13}{12}\)
Since, y lies in the 2nd quadrant, the value of sec y will be negative.
Therefore, sec y = \(– \frac{13}{12}\)
cos y = \(\frac{1}{sec \; y } = \frac{1}{\left (- \frac{13}{12} \right )} = \left (- \frac{12}{13} \right )\\\)
Since, \(tan \; y = \frac{sin \; y}{cos \; y}\)
\(\Rightarrow\) \( -\frac{5}{12} = \frac{sin \; y}{\left (- \frac{12}{13} \right )}\\\)
\(\Rightarrow\) sin y = \(\left (-\frac{5}{12} \right ) \times \left (- \frac{12}{13}\right ) = \frac{5}{13}\\\)
\(\Rightarrow\) cosec y = \(\frac{1}{sin \; y} = \frac{1}{\left ( \frac{5}{13} \right )} = \frac{13}{5}\)
Q.6: Calculate the value of trigonometric function sin 765°.
Sol:
The values of sin y repeat after an interval of 360° or 2n.
Therefore, sin 765° = sin ( 2 × 360° + 45° ) = sin 45° = \(\frac{1}{\sqrt{2}}\)
Q.7: Calculate the value of trigonometric function cosec [-1410°]
Sol:
It is known that the values of tan y repeat after an interval of 360° or 2n.
Therefore, cosec [-1410°] = cosec [-1410° + 4 × 360°] = cosec [ -1410° + 1440°] = cosec 30° = 2
Q.8: Calculate the value of the trigonometric function \(\tan \frac{19\pi }{3}\).
Sol:
It is known that the values of tan y repeat after an interval of 360° or 2n.
Therefore, \(\tan \frac{19\pi }{3}\) = \(\tan 6\frac{1}{3}\pi\) = \(\tan \left ( 6\pi + \frac{\pi }{3} \right )\) = \(\tan \frac{\pi }{3}\) = tan 60° = \(\sqrt{3}\)
Q.9: Calculate the value of the trigonometric function \(\sin \left ( -\frac{11\pi }{3} \right )\).
Answer:
It is known that the values of tan y repeat after an interval of 360° or 2n.
Therefore, \(\sin \left ( -\frac{11\pi }{3} \right )\) = \(\sin \left ( -\frac{11\pi }{3} + 2 \times 2\pi \right )\) = \(\sin \frac{\pi }{3}\) = \(\frac{\sqrt{3}}{2}\)
Q.10: Calculate the value of the trigonometric function \(\cot \left ( -\frac{15\pi }{4} \right )\).
Sol:
It is known that the values of \(\tan y\) repeat after an interval of \(180^{\circ}\) or n.
Therefore, \(\cot \left ( -\frac{15\pi }{4} \right )\) = \(\cot \left ( -\frac{15\pi }{4} + 4\pi \right )\) = \(\cot \frac{\pi }{4}\) = 1
Exercise 3.3
Q.1: Prove:
\(\sin ^{2} \frac{\pi }{6} + \cos ^{2} \frac{\pi }{3} – \tan ^{2} \frac{\pi }{4} = -\frac{1}{2}\)
Sol:
Now, taking L.H.S.
\(\sin ^{2} \frac{\pi }{6} + \cos ^{2} \frac{\pi }{3} – \tan ^{2} \frac{\pi }{4}\):
= \(\\\left (\frac{1}{2} \right )^{2} + \left (\frac{1}{2} \right )^{2} – \left ( 1 \right )^{2}\)
= \(\\\frac{1}{4} + \frac{1}{4} – 1\) = \(-\frac{1}{2}\)
= R.H.S.
Q.2: Prove:
\(2 \sin ^{2} \frac{\pi }{6} + cosec^{2}\frac{7\pi }{6} \cos ^{2}\frac{\pi }{3} = \frac{3}{2}\)
Sol:
Now, taking L.H.S.
\(2 \sin ^{2} \frac{\pi }{6} + cosec^{2}\frac{7\pi }{6} \cos ^{2}\frac{\pi }{3}\\\) :
= \(\\2 \left (\frac{1}{2} \right )^{2} + cosec ^{2}\left ( \pi + \frac{\pi }{6} \right )\left ( \frac{1}{2} \right )^{2}\)
= \(2 \times \frac{1}{4} + \left (-cosec \frac{\pi }{6} \right )^{2}\left ( \frac{1}{4} \right )\)
= \(\frac{1}{2} + \left ( -2 \right )^{2}\left ( \frac{1}{4} \right )\)
= \(\frac{1}{2} + \frac{4}{4}\)
= \(\frac{1}{2} + 1\)
= \(\frac{3}{2}\)
= R.H.S.
Q.3: Prove:
\(\cot ^{2}\frac{\pi }{6} + cosec \frac{5\pi }{6} + 3\tan ^{2} \frac{\pi }{6} = 6\)
Sol:
Taking L.H.S.
\(\cot ^{2}\frac{\pi }{6} + cosec \frac{5\pi }{6} + 3\tan ^{2} \frac{\pi }{6}\\\) :
= \(\left (\sqrt{3} \right )^{2} + cosec \left ( \pi – \frac{\pi }{6} \right ) + 3\left ( \frac{1}{\sqrt{3}} \right )^{2}\)
= \(3 + cosec \frac{\pi }{6} + 3\times \frac{1}{3}\)
= 3 + 2 + 1 = 6
= R.H.S.
Q.4: Prove:
\(2\sin ^{2} \frac{3\pi }{4} + 2\cos ^{2} \frac{\pi }{4} + 2\sec ^{2} \frac{\pi }{3} = 10\)
Sol:
Now, taking L.H.S.
\(2\sin ^{2} \frac{3\pi }{4} + 2\cos ^{2} \frac{\pi }{4} + 2\sec ^{2} \frac{\pi }{3}\\\) :
= \(\\2\left \{ \sin \left ( \pi – \frac{\pi }{4} \right ) \right \}^{2} + 2\left (\frac{1}{\sqrt{2}} \right )^{2} + 2\left ( 2 \right )^{2}\)
= \(2\left \{ \sin \frac{\pi }{4} \right \}^{2} + 2\times \frac{1}{2} + 8\)
= \(2\left ( \frac{1}{\sqrt{2}} \right )^{2}\) + 1 + 8
= 1 + 1 + 8 = 10
= R.H.S.
Q.5: Calculate the value of:
(i). \(\sin 75^{\circ}\)
(ii). \(\tan 15^{\circ}\)
Sol:
(i). \(\sin 75^{\circ}\):
= \(\sin \left ( 45^{\circ} + 30^{\circ} \right )\)
= \(\sin 45^{\circ} \cos 30^{\circ} + \cos 45^{\circ} \sin 30^{\circ}\)
Since, [sin (x + y) = sin x cos y + cos x sin y]
= \(\left (\frac{1}{\sqrt{2}} \right )\left (\frac{\sqrt{3}}{2} \right ) + \left (\frac{1}{\sqrt{2}} \right )\left ( \frac{1}{2} \right )\)
= \(\frac{\sqrt{3}}{2\sqrt{2}} + \frac{1}{2\sqrt{2}}\)
= \(\frac{\sqrt{3} + 1}{2\sqrt{2}}\)
(ii). \(\tan 15^{\circ}\):
= \(\tan \left ( 45^{\circ} – 30^{\circ}\right )\)
= \(\frac{\tan 45^{\circ} – \tan 30^{\circ}}{1 + \tan 45^{\circ}\tan 30^{\circ}}\)
Since, [tan (x – y) = \(\frac{\tan x – \tan y}{1 + \tan x \tan y}\)]
= \(\\\frac{1 – \frac{1}{\sqrt{3}}}{1 + 1\left ( \frac{1}{\sqrt{3}} \right )}\)
= \(\\\frac{\frac{\sqrt{3} – 1}{\sqrt{3}}}{\frac{\sqrt{3 + 1}}{\sqrt{3}}}\)
= \(\\\frac{\sqrt{3} – 1}{\sqrt{3} + 1}\)
= \(\\\frac{\left ( \sqrt{3} – 1\right )^{2}}{\left ( \sqrt{3} + 1\right )\left ( \sqrt{3} – 1 \right )}\)
= \(\\\frac{3 + 1 – 2\sqrt{3}}{\left ( \sqrt{3} \right )^{2} – \left ( 1 \right )^{2}}\)
= \(\frac{4 – 2\sqrt{3}}{3 – 1}\)
= \(2 – \sqrt{3}\)
Q.6:Prove:
\(\cos \left ( \frac{\pi }{4} – x\right ) \cos \left ( \frac{\pi }{4} – y\right ) – \sin \left ( \frac{\pi }{4} – x\right ) \sin \left ( \frac{\pi }{4} – y\right ) = \sin \left ( x+y \right )\)
Sol:
Now, taking L.H.S.
\(\cos \left ( \frac{\pi }{4} – x\right ) \cos \left ( \frac{\pi }{4} – y\right ) – \sin \left ( \frac{\pi }{4} – x\right ) \sin \left ( \frac{\pi }{4} – y\right ):\\\)
= \(\\\frac{1}{2}\left [ 2\cos \left ( \frac{\pi }{4} – x \right ) \cos \left ( \frac{\pi }{4} – y \right ) \right ] + \frac{1}{2}\left [ -2\sin \left ( \frac{\pi }{4} – x \right ) \sin \left ( \frac{\pi }{4} – y \right ) \right ]\\\)
\(=\frac{1}{2}\left [ \cos \left \{ \left ( \frac{\pi }{4} – x \right ) + \left ( \frac{\pi }{4} – y \right )\right \} + \cos \left \{ \left ( \frac{\pi }{4} – x \right ) – \left ( \frac{\pi }{4} – y \right )\right \}\right ] + \frac{1}{2}\left [ \cos \left \{ \left ( \frac{\pi }{4} – x \right ) + \left ( \frac{\pi }{4} – y \right )\right \} – \cos \left \{ \left ( \frac{\pi }{4} – x \right ) – \left ( \frac{\pi }{4} – y \right )\right \}\right ]\\\)
Since, [2cos A cos B = cos (A + B) + cos (A – B)]
And, [2sin A sin B = cos (A + B) – cos (A – B)]
= \(\\2\times \frac{1}{2}\left [ \cos \left \{ \left ( \frac{\pi }{4} – x \right ) + \left ( \frac{\pi }{4} – y \right ) \right \} \right ]\\\)
= \(\\\cos \left [ \frac{\pi }{2} – \left ( x + y \right )\right ]\)
= sin (x + y)
= R.H.S.
Q.7: Prove:
\(\frac{\tan \left ( \frac{\pi }{4} + x\right )}{\tan \left ( \frac{\pi }{4} – x\right )} = \left (\frac{1 + \tan x}{1 – \tan x} \right )^{2}\)
Sol:
Since, tan (A + B)= \(\frac{\tan A + \tan B}{1 – \tan A\tan B}\\\)
And, tan (A – B) = \(\frac{\tan A – \tan B}{1 + \tan A\tan B}\)
Now, taking L.H.S.
\(\frac{\tan \left ( \frac{\pi }{4} + x\right )}{\tan \left ( \frac{\pi }{4} – x\right )}\\\):
= \(\\\frac{\left (\frac{\tan \frac{\pi }{4} + \tan x}{1 – \tan \frac{\pi }{4} \tan x} \right )}{\left (\frac{\tan \frac{\pi }{4} – \tan x}{1 + \tan \frac{\pi }{4} \tan x} \right )}\\\)
= \(\\\frac{\left (\frac{1 + \tan x}{1 – \tan x} \right )}{\left (\frac{1 – \tan x}{1 + \tan x} \right )}\\\)
= \(\\\left (\frac{1 + \tan x}{1 – \tan x} \right )^{2}\)
= R.H.S.
Q.8: Prove:
\(\frac{\cos \left ( \pi + x \right ) \cos \left ( -x \right )}{\sin \left ( \pi – x \right ) \cos \left ( \frac{\pi }{2} + x \right )} = \cot ^{2} x\)
Sol:
Now, taking L.H.S.
\(\frac{\cos \left ( \pi + x \right ) \cos \left ( -x \right )}{\sin \left ( \pi – x \right ) \cos \left ( \frac{\pi }{2} + x \right )}\\\):
= \(\\\frac{\left [ -\cos x \right ]\left [ \cos x \right ]}{\left ( \sin x \right )\left ( -\sin x \right )}\\\)
= \(\\\frac{-\cos ^{2} x}{-\sin ^{2} x}\) = \(\cot ^{2} x\)
= R.H.S.
Q.9: Prove:
\(\cos \left ( \frac{3\pi }{2} + x\right ) \cos \left ( 2\pi + x \right )\left [ \cot \left ( \frac{3\pi }{2} – x\right ) + \cot \left ( 2\pi + x \right ) \right ] = 1\)
Sol:
Now, taking L.H.S.
\(\cos \left ( \frac{3\pi }{2} + x\right ) \cos \left ( 2\pi + x \right )\left [ \cot \left ( \frac{3\pi }{2} – x\right ) + \cot \left ( 2\pi + x \right ) \right ]\\\):
= \(\\\sin x\cos x \left [ \tan x + \cot x \right ]\\\)
= \(\\\sin x\cos x \left ( \frac{\sin x}{\cos x} + \frac{\cos x}{\sin x} \right )\\\)
= \(\\\left (\sin x\cos x \right )\left [ \frac{\sin ^{2} x + \cos ^{2} x}{\sin x \cos x} \right ]\\\)
= \(\\\sin ^{2} x + \cos ^{2} x\) = 1
= R.H.S.
Q.10: Prove:
\(\sin \!\left ( n + 1 \right )\!x \; \sin\! \left ( n + 2 \right )\!x + \cos \! \left ( n + 1 \right )\! x \cos \! \left ( n + 2 \right )\! x = \cos x\)
Sol:
Now, taking L.H.S.
\(\sin \!\left ( n + 1 \right )\!x \; \sin\! \left ( n + 2 \right )\!x + \cos \! \left ( n + 1 \right )\! x \cos \! \left ( n + 2 \right )\! x:\\\)
=\(\\\frac{1}{2}\left [ 2\sin \! \left ( n + 1 \right ) \! x \sin \! \left ( n + 2 \right ) \! x + 2\cos \! \left ( n + 1 \right ) \! x \cos \! \left ( n + 2 \right ) \! x\right ]\\\)
=\(\\\frac{1}{2}\left [ \cos \left \{ \left ( n + 1 \right )x – \left ( n + 2 \right )x \right \} – \cos \left \{ \left ( n + 1 \right )x + \left ( n + 2 \right )x \right \} + \cos \left \{ \left ( n + 1 \right )x + \left ( n + 2 \right )x \right \} + \cos \left \{ \left ( n + 1 \right )x – \left ( n + 2 \right )x \right \}\right ]\\\)
Since, [2sin A sin B = cos (A + B) – cos (A – B)]
And, [2cos A cos B = cos (A + B) + cos (A – B)]
= \(\\\frac{1}{2}\times 2 \cos \left \{ \left ( n + 1 \right )x – \left ( n + 2 \right )x \right \}\\\)
= \(\\\cos \left ( -x \right )\) = cos x
= R.H.S.
Q.11 Prove:
\(\cos \left ( \frac{3\pi }{4} + x\right ) – \cos \left ( \frac{3\pi }{4} – x\right ) = -\sqrt{2}\sin x\)
Sol:
Since, cos A – cos B = \(-2\sin \left ( \frac{A + B}{2} \right )\sin \left ( \frac{A – B}{2} \right )\)
Now, taking L.H.S.
\(\cos \left ( \frac{3\pi }{4} + x\right ) – \cos \left ( \frac{3\pi }{4} – x\right ):\\\)
= \(\\-2\sin \left \{ \frac{\left ( \frac{3\pi }{4} + x \right ) + \left ( \frac{3\pi }{4} – x \right )}{2} \right \} sin \left \{ \frac{\left ( \frac{3\pi }{4} + x \right ) – \left ( \frac{3\pi }{4} – x \right )}{2} \right \}\\\)
= \(\\-2\sin \left ( \frac{3\pi }{4} \right )\sin x\)
= \(\\-2\sin \left ( \pi – \frac{\pi }{4} \right )\sin x\)
= \(\\-2\sin \frac{\pi }{4} \sin x\)
= \(\\-2 \times \frac{1}{\sqrt{2}} \times \sin x\)
= \(\\-\sqrt{2} \sin x\)
= R.H.S.
Q.12: Prove:
\(\sin ^{2} 6x – \sin ^{2} 4x = \sin\! 2x \; \sin \! 10x\)
Sol:
Since, sin A + sin B = \(2\sin \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
And, sin A – sin B = \(2\cos \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
Now, taking L.H.S.
\(\sin ^{2} 6x – \sin ^{2} 4x\\\):
= \(\\\left (\sin 6x + \sin 4x \right )\left ( \sin 6x – \sin 4x \right )\)
= \(\\\left [ 2\sin \left ( \frac{6x + 4x}{2} \right ) \cos \left ( \frac{6x – 4x}{2} \right ) \right ] \left [ 2\cos \left ( \frac{6x + 4x}{2} \right ) \sin \left ( \frac{6x – 4x}{2} \right ) \right ]\)
= (2sin 5x cos x) (2cos 5x sin x)
= (2 sin 5x cos 5x) (2 cos x sin x)
= sin 10x sin 2x
= R.H.S.
Q.13: Prove:
\(\cos ^{2} 2x – \cos ^{2} 6x = \sin 4x \sin 8x\)
Sol:
Since, cos A + cos B = \(2\cos \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
And, cos A – cos B = \(2\sin \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
Now, taking L.H.S.
\(\cos ^{2} 2x – \cos ^{2} 6x\):
= (cos 2x + cos 6x) (cos 2x – cos 6x)
= \(\\\left [ 2\cos \left ( \frac{2x + 6x}{2} \right ) \cos \left ( \frac{2x – 6x}{2} \right ) \right ] \left [ -2 \sin \left ( \frac{2x + 6x}{2} \right ) \sin \left ( \frac{2x – 6x}{2} \right ) \right ]\\\)
= [2cos 4x cos (-2x)] [ -2sin 4x sin ( -2x)]
= [2cos 4x cos 2x] [-2sin 4x ( -sin2x)]
= [2sin 4x cos 4x] [2sin 2x cos 2x]
= sin 8x sin 4x
= R.H.S.
Q.14:Prove:
\(\sin 2x + 2\sin 4x + \sin 6x = 4 \cos ^{2} x \sin 4x\)
Sol:
Now, taking L.H.S.
sin 2x + 2sin 4x + sin 6x:
= [sin 2x + sin 6x] + 2 sin 4x
= \(\\\left [ 2 \sin \left (\frac{2x + 6x}{2} \right ) \left (\frac{2x – 6x}{2} \right ) \right ] + 2 \sin 4x\\\)
Since, sin A + sin B = \(2\sin \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
= 2sin 4x cos(-2x) + 2sin 4x
= 2sin 4x cos 2x + 2sin 4x
= 2sin 4x (cos 2x + 1)
= \(2 \sin 4x \; \left ( 2 \cos ^{2} x – 1 + 1\right )\)
= \(2 \sin 4x \; \left ( 2 \cos ^{2} x \right )\)
= \(4 \cos ^{2} x \sin 4x\)
= R.H.S.
Q.15: Prove:
\(\cot 4x \left ( \sin 5x + \sin 3x \right ) = \cot x \left ( \sin 5x – \sin 3x \right )\)
Sol:
Now, taking L.H.S.
cot 4x (sin 5x + sin 3x):
= \(\frac{\cos 4x}{\sin 4x} \left [ 2 \sin \left ( \frac{5x + 3x}{2} \right ) \cos \left ( \frac{5x – 3x}{2} \right ) \right ]\)
Since, sin A – sin B = \(2\cos \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
= \(\left ( \frac{\cos 4x}{\sin 4x} \right )\left [ 2 \sin 4x \; \cos x \right ]\)
=2cos 4x cos x . . . . . . . . . . . . . . . (1)
Now, taking R.H.S.
cot x (sin 5x – sin 3x):
= \(\frac{\cos x}{\sin x} \left [ 2 \cos \left ( \frac{5x + 3x}{2} \right ) \sin \left ( \frac{5x – 3x}{2} \right ) \right ]\)
\(\sin A – \sin B = 2\cos \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
= \(\frac{\cos x}{\sin x} \left [ 2 \cos 4x\; \sin x \right ]\)
= 2 cos 4x cos x . . . . . . . . . . . . . . . . . . . . (2)
From equation (1) and (2):
L.H.S. = R.H.S.
Q.16: Prove:
\(\frac{\cos 9x – \cos 5x}{\sin 17x – \sin 3x} = -\frac{\sin 2x}{\cos 10x}\)
Sol:
Since, cos A – cos B = \(2\sin \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
And, sin A – sin B = \(2\cos \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
Now, taking L.H.S.
\(\frac{\cos 9x – \cos 5x}{\sin 17x – \sin 3x}:\\\)
= \(\\\frac{-2 \sin \left (\frac{9x + 5x}{2} \right )\; \sin \left (\frac{9x – 5x}{2} \right )}{2\cos \left (\frac{17x + 3x}{2} \right ) \; \sin \left (\frac{17x – 3x}{2} \right )}\\\)
= \(\\\frac{-2 \sin 7x \; \sin 2x}{2 \cos 10x \; \sin 7x}\\\)
= \(\\-\frac{\sin 2x}{\cos 10x}\)
= R.H.S.
Q.17: Prove:
\(\frac{\sin 5x + \sin 3x}{\cos 5x + \cos 3x} = \tan 4x\)
Sol:
Since, sin A + sin B = \(2\sin \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
And, cos A + cos B = \(2\cos \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
Now, taking L.H.S.
\(\frac{\sin 5x + \sin 3x}{\cos 5x + \cos 3x}\\\):
= \(\\\frac{2 \sin \left ( \frac{5x + 3x}{2} \right ) \; \cos \left ( \frac{5x – 3x}{2} \right ) }{2 \cos \left ( \frac{5x + 3x}{2} \right ) \; \cos \left ( \frac{5x – 3x}{2} \right )}\\\)
= \(\\\frac{2 \sin 4x \cos x}{2 \cos 4x \cos x}\) = tan 4x
=R.H.S.
Q.18: Prove:
\(\frac{\sin x – \sin y}{\cos x + \cos y} = \tan \frac{x – y}{2}\)
Sol:
Since, cos A + cos B = \(2\cos \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
And, sin A – sin B = \(2\cos \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
Now taking L.H.S.
\(\frac{\sin x – \sin y}{\cos x + \cos y}:\\\)
= \(\\\frac{2 \cos \left ( \frac{x + y}{2} \right ) \;\sin \left ( \frac{x – y}{2} \right )}{2 \cos \left ( \frac{x + y}{2} \right ) \;\cos \left ( \frac{x – y}{2} \right )}\\\)
= \(\\\frac{\sin \left ( \frac{x – y}{2} \right )}{\cos \left ( \frac{x – y}{2} \right )}\)
= \(\\\tan \left ( \frac{x – y}{2} \right )\)
= R.H.S.
Q.19: Prove:
\(\frac{\sin x + \sin 3x}{\cos x + \cos 3x} = \tan 2x\)
Sol::
Since, sin A + sin B = \(2\sin \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
And, cos A + cos B = \(2\cos \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
Now, taking L.H.S.
\(\frac{\sin x + \sin 3x}{\cos x + \cos 3x}:\\\)
= \(\\\frac{2 \sin \left ( \frac{x + 3x}{2} \right ) \;\cos \left ( \frac{x – 3x}{2} \right )}{2 \cos \left ( \frac{x + 3x}{2} \right ) \;\cos \left ( \frac{x – 3x}{2} \right )}\)
= \(\\\frac{\sin 2x}{\cos 2x}\) = tan 2x
= R.H.S.
Q.20: Prove:
\(\frac{\sin x – \sin 3x}{\sin ^{2} x – \cos ^{2} x} = 2\sin x\)
Answer:
Since, sin A – sin B = \(2\cos \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
\(\cos ^{2} A – \sin ^{2} A = \cos 2A\\\)
Now, taking L.H.S.
\(\frac{\sin x – \sin 3x}{\sin ^{2} x – \cos ^{2} x}\\\):
= \(\\\frac{2 \cos \left (\frac{x + 3x}{2} \right ) \sin \left ( \frac{x – 3x}{2} \right )}{ – \cos 2x}\\\)
= \(\\\frac{2 \cos 2x \;\sin \left ( -x \right )}{-\cos 2x}\\\)
= \(\\-2x \left ( -\sin x \right )\) = 2 sin x
= R.H.S.
Q.21: Prove:
\(\frac{\cos 4x + \cos 3x + \cos 2x}{\sin 4x + \sin 3x + \sin 2x} = \cot 3x\)
Sol:
Taking L.H.S.
\(\frac{\cos 4x + \cos 3x + \cos 2x}{\sin 4x + \sin 3x + \sin 2x}\):
= \(\\\frac{\left (\cos 4x + \cos 2x \right )+ \cos 3x}{\left (\sin 4x + \sin 2x \right ) + \sin 3x}\\\)
= \(\\\frac{2 \cos \left ( \frac{4x + 2x}{2} \right ) \cos \left ( \frac{4x – 2x}{2} \right ) + \cos 3x}{2 \sin \left ( \frac{4x + 2x}{2} \right ) \cos \left ( \frac{4x – 2x}{2} \right ) + \sin 3x}\\\)
\(\\\begin{bmatrix} \sin A + \sin B = 2\sin \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\\* \cos A + \cos B = 2\cos \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\\ \end{bmatrix}\)
= \(\frac{2 \cos 3x \; \cos x + \cos 3x}{2 \sin 3x \; \cos x + \sin 3x}\\\)
= \(\\\frac{\cos 3x \left ( 2 \cos x + 1 \right )}{\sin 3x \left ( 2 \cos x + 1 \right )}\) = cot 3x
= R.H.S.
Q.22: Prove:
\(\cot x \;\cot 2x – \cot 2x \;\cot 3x – \cot 3x \;\cot x = 1\)
Sol:
Now, taking L.H.S.
cot x cot 2x – cot 2x cot 3x – cot 3x cot x :
= \(\\\cot x \;\cot 2x – \cot 3x\left ( \cot 2x + \cot x \right )\\\)
= \(\\\cot x \;\cot 2x – \cot\left ( 2x + x \right )\left ( \cot 2x + \cot x \right )\\\)
= \(\\\cot x \;\cot 2x – \left [ \frac{\cot 2x \;\cot x – 1}{\cot x + \cot 2x} \right ]\left ( \cot 2x + \cot x \right )\\\)
= \(\\\left [\cot \left ( A + B \right ) = \frac{\cot A \; \cot B – 1}{\cot A + \cot B} \right ]\\\)
= \(\\\cot x \;\cot 2x – \left ( \cot 2x \cot x – 1 \right )\) = 1
= R.H.S
Q.23: Prove:
\(\tan 4x = \frac{4 \tan x \left ( 1 – \tan ^{2}x \right )}{1 – 6\tan ^{2} x + \tan ^{4} x}\)
Sol:
Since, tan 2A = \(\frac{2\tan A}{1 – \tan ^{2}A}\)
Now, taking L.H.S.
tan 4x :
= \(\tan 2\left (2x \right )\)
= \(\\\frac{2 \tan 2x}{1 – \tan ^{2}\left (2x \right )}\\\)
= \(\\\frac{2 \left ( \frac{2 \tan x}{1 – \tan ^{2}x} \right )}{1 – \left ( \frac{2 \tan x}{1 – \tan ^{2}x} \right )^{2}}\\\)
= \(\\\frac{\left ( \frac{4 \tan x}{1 – \tan ^{2}x} \right )}{1 – \left ( \frac{4 \tan ^{2}x}{\left (1 – \tan ^{2}x \right )^{2}} \right )}\\\)
= \(\\\frac{\left (\frac{4\tan x}{1 – \tan ^{2}x} \right )}{\left [\frac{\left ( 1 – \tan ^{2}x \right )^{2} – 4 \tan ^{2}x}{\left ( 1 – \tan ^{2}x \right )^{2}} \right ]}\\\)
= \(\\\frac{4 \tan x \left ( 1 – \tan ^{2} x\right )}{\left ( 1 – \tan ^{2}x \right )^{2} – 4 \tan ^{2} x}\\\)
= \(\\\frac{4 \tan x \left ( 1 – \tan ^{2}x \right )}{1 + \tan ^{4}x – 2 \tan ^{2}x – 4 \tan ^{2}x}\\\)
= \(\\\frac{4 \tan x \left ( 1 – \tan ^{2}x \right )}{1 – 6 \tan ^{2}x + \tan ^{4}x }\)
= R.H.S.
Q.24: Prove:
\(\cos 4x = 1 – 8 \sin ^{2}x \;\cos ^{2}x\)
Sol:
Now, taking L.H.S.
cos 4x:
= \(\\\cos 2\left (2x \right )\\\)
= \(\\1 – 2 \sin ^{2} 2x \;\;\;\;\left [ \cos 2A = 1 – 2 \sin ^{2}A \right ]\\\)
= \(\\1 – 2 \left ( 2 \sin x \cos x \right )^{2} \;\;\;\;\;\left [ \sin 2A = 2 \sin A \cos A \right ]\\\)
= \(\\1 – 8 \sin ^{2}x \cos ^{2}x\\\)
= R.H.S.
Q.25: Prove:
\(\cos 6x = 32 \cos ^{6}x – 48 \cos ^{4}x + 18 \cos ^{2}x -1\)
Sol:
Now, taking L.H.S.
cos 3 (2x ):
= \(\\4 \cos ^{3}2x – 3 \cos 2x \;\;\;\;\; \left [ \cos 3A = 4\cos ^{3}A – 3 \cos A \right ]\\\)
= \(\\4 \left ( 2 \cos ^{2}x – 1 \right )^{3} – 3 \left ( 2 \cos ^{2}x -1 \right ) \;\;\;\;\; \left [ \cos 2x = 2 \cos ^{2}x -1 \right ]\\\)
= \(\\4 \left [ \left ( 2 \cos ^{2}x \right )^{3} – \left (1 \right )^{3} – 3 \left ( 2 \cos ^{2}x \right )^{2} + 3 \left ( 2 \cos ^{2}x \right )\right ] – 6 \cos ^{2}x + 3\\\)
= \(\\4 \left [ 8 \cos ^{6}x – 1 – 12\cos ^{4}x + 6 \cos ^{2}x \right ] – 6 \cos ^{2}x + 3\\\)
= \(\\32 \cos ^{6}x – 4 – 48 \cos ^{4}x + 24 \cos ^{2}x – 6 \cos ^{2}x + 3\\\)
= \(\\32 \cos ^{6}x – 48 \cos ^{4}x + 18 \cos ^{2}x -1\)
= R.H.S.
Exercise 3.4
Q.1: Find general solutions and the principle solutions of the given equation: tan x = \(\sqrt{3}\)
Sol:
tan x = \(\sqrt{3}\) [Given]
As we know that, \(\tan \frac{\pi }{3} = \sqrt{3}\)
And, \(\tan \frac{4\pi }{3}\) = \(\tan \left ( \pi + \frac{\pi }{3} \right )\) = \(\tan \left ( \frac{\pi }{3} \right )\) = \(\sqrt{3}\)
Therefore, the principle solutions are \(x = \frac{\pi }{3}\) and \(\frac{4\pi }{3}\)
Now, \(\tan x = \tan \frac{\pi }{3}\\\)
\(x = n\pi + \frac{\pi }{3}\), where n \(\in\) Z
Therefore, the general solution is \(x = n\pi + \frac{\pi }{3}\), where n \(\in\) Z.
Q.2: Find general solutions and the principle solutions of the given equation: sec x = 2
Sol:
sec x = 2 [Given]
As we know that, \(\sec \frac{\pi }{3} = 2\)
And, \(\sec \frac{5\pi }{3}\) = \(\sec \left (2\pi – \frac{\pi }{3} \right )\) = \(\sec \frac{\pi }{3}\) = 2
Therefore, the principle solutions are \(x = \frac{\pi }{3}\) and \(\frac{5\pi }{3}\).
Now, \(\sec x = \sec \frac{\pi }{3}\)
And, \(\cos x = \cos \frac{\pi }{3} \;\;\;\;\; \left [ \sec x = \frac{1}{\cos x} \right ]\\\)
\(x = 2n\pi \pm \frac{\pi }{3}\), where n \(\in\) Z
Therefore, the general solution is \(x = 2n\pi \pm \frac{\pi }{3}\), where n \(\in\) Z.
Q.3: Find general solutions and the principle solutions of the given equation:
cot = \( -\sqrt{3}\)
Sol:
cot = \(-\sqrt{3}\) [Given]
As we know that, \(\cot \frac{\pi }{6} = \sqrt{3}\;\;\Rightarrow \;\;\cot \left (\pi – \frac{\pi }{6} \right ) = -\cot \frac{\pi }{6} = -\sqrt{3}\)
And, \(\cot \left ( 2\pi – \frac{\pi }{6} \right )\) = \(-\cot \frac{\pi }{6}\) = \(-\sqrt{3}\)
That is \(\cot \frac{5\pi }{6} = -\sqrt{3}\) and \(\cot \frac{11\pi }{6} = -\sqrt{3}\)
Therefore, the principle solutions are \(x = \frac{5\pi }{6}\) and \(\frac{11\pi }{6}\).
Now,\(\cot x = \cot \frac{5\pi }{6}\)
And, \(\tan x = \tan \frac{5\pi }{6} \;\;\;\;\;\left [ \cot x = \frac{1}{\tan x} \right ]\)
\(\\x = n\pi + \frac{5\pi }{6}\), where n \(\in\) Z
Therefore, the general solution is \(x = n\pi + \frac{5\pi }{6}\), where n \(\in\) Z.
Q.4: Find general solutions and the principle solutions of the given equation: cosec x = -2
Sol:
cosec x = -2 [Given]
As we know that, \(cosec \frac{\pi }{6} = 2\)
Hence, \(cosec \left (\pi + \frac{\pi }{6} \right )\) = \(-cosec \frac{\pi }{6}\) = -2
And, \(cosec \left (2\pi – \frac{\pi }{6} \right )\) = \(-cosec \frac{\pi }{6}\) = -2
That is \(cosec \frac{7\pi }{6} = -2\) and \(cosec \frac{11\pi }{6} = -2\).
Therefore, the principle solutions are \(x = \frac{7\pi }{6}\) and \(\frac{11\pi }{6}\).
Now,\(cosec \: x = cosec \frac{7\pi }{6}\)
And, \(\sin x = \sin \frac{7\pi }{6} \;\;\;\;\; \left [ cosec x = \frac{1}{\sin x} \right ]\)
\(\\x = n\pi + \left ( -1 \right )^{n}\frac{7\pi }{6}\), where n \(\in\) Z
Therefore, the general solution is \(x = n\pi + \left ( -1 \right )^{n}\frac{7\pi }{6}\), where n \(\in\) Z.
Q.5: Find the general solution of the given equation: cos 4x = cos 2x
Sol:
cos 4x = cos 2x [Given]
i.e. cos 4x – cos 2x = 0
\(-2\sin \left ( \frac{4x + 2x}{2} \right ) \sin \left ( \frac{ 4x – 2x }{2}\right ) = 0\)
Since, cos A – cos B = \(2\sin \left ( \frac{A + B}{2} \right ) \sin \left ( \frac{A – B}{2} \right )\)
(sin 3x) (sin x) = 0
sin 3x = 0 or sin x = 0
sin 3x = 0
\(3x = n\pi\\\)
\(x = \frac{n\pi}{3}\), where n \(\in\) Z
sin x = 0
\(\Rightarrow\) \(x = n\pi\), where n \(\in\) Z
Q.6: Find the general solution of the given equation: cos 3x + cos x – cos 2x = 0
Sol:
cos 3x + cos x – cos 2x = 0 [Given]
\(2 \cos \left ( \frac{3x + x}{2} \right ) \cos \left ( \frac{3x – x}{2} \right ) – \cos 2x = 0\)
Since, cos A + cos B = \(2\cos \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
2cos 2x cos x – cos 2x = 0
cos 2x (2cos x – 1) = 0
cos 2x = 0 or 2cos x -1 = 0
cos 2x = 0
\(2x = \left ( 2n + 1 \right )\frac{\pi }{2}\), where n \(\in\) Z
\(\\x = \left ( 2n + 1 \right )\frac{\pi }{4}\), where n \(\in\) Z
2cos x -1 = 0
\(\cos x = \frac{1}{2}\\\)
\(\cos x = \cos \frac{\pi }{3}\), where n \(\in\) Z
\(x = 2n\pi \pm \frac{\pi }{3}\), where n \(\in\) Z
Q.7: Find the general solution of the given equation: sin 2x + cos x = 0
Sol:
sin 2x + cos x = 0 [Given]
2sin x cos x + cos x = 0
cos x (2sin x + 1) = 0
cos x = 0 or 2sin x + 1 = 0
cos x = 0
\(\cos x = \left ( 2n + 1 \right )\frac{\pi }{2}\), where n \(\in\) Z
2sin x + 1 = 0
= \(-\sin \frac{\pi }{6}\) = \(\sin \left (\pi + \frac{\pi }{6} \right )\) = \(\sin \frac{7\pi }{6}\)
\(\Rightarrow\) \(x = n\pi + \left ( -1 \right )^{n}\frac{7\pi }{6}\), where n \(\in\) Z
Therefore, the general solution is \(\\\left ( 2n + 1 \right )\frac{\pi }{2}\) or \(n\pi + \left ( -1 \right )^{n}\frac{7\pi }{6}\), where n \(\in\) Z.
Q.8: Find the general solution of the given equation:
\(\sec ^{2}2x = 1 – \tan 2x\)
Sol:
\(\sec ^{2}2x = 1 – \tan 2x\) [Given]
\(1 + \tan ^{2}2x = 1 – \tan 2x\) \(\tan ^{2}2x + \tan 2x = 0\)
tan 2x ( tan 2x + 1) = 0
tan 2x = 0 or tan 2x + 1 = 0
tan 2x = 0
tan 2x = tan 0
2x = n? + 0, where n \(\in\) Z
\(x = \frac{n\pi}{2}\), where n \(\in\) Z
tan 2x + 1 = 0
tan 2x = -1= \(-\tan \frac{\pi }{4}\)= \(\tan \left (\pi – \frac{\pi }{4} \right )\)= \(\tan \frac{3\pi }{4}\)
\(\Rightarrow\) \(2x = n\pi + \frac{3\pi }{4}\), where n \(\in\) Z
\(\Rightarrow\) \(x = \frac{n\pi}{2} + \frac{3\pi }{8}\), where n \(\in\) Z
Therefore, the general solution is \(\frac{n\pi}{2}\) or \(\frac{n\pi}{2} + \frac{3\pi }{8}\), where n \(\in\) Z.
Q.9: Find the general solution of the given equation: sin x + sin 3x + sin 5x = 0
Sol:
sin x + sin 3x + sin 5x = 0 [Given]
(sin x + sin 5x) + sin 3x = 0
\(\left [ 2\sin \left ( \frac{x + 5x}{2} \right ) \cos \left ( \frac{x – 5x}{2} \right )\right ] + \sin 3x = 0\)
Since, sin A + sin B = \(2\sin \left ( \frac{A + B}{2} \right ) \cos \left ( \frac{A – B}{2} \right )\)
2sin 3x cos (-2x) + \sin 3x = 0
2sin 3x cos 2x + sin 3x = 0
sin 3x (2cos 2x + 1) = 0
sin 3x = 0 or 2cos 2x + 1 = 0
Now,
sin 3x = 0
\(3x = n\pi\), where n \(\in\) Z
\(x = \frac{n\pi }{3}\), where n \(\in\) Z
2cos 2x + 1 = 0
\(\cos 2x = -\frac{1}{2}\) = \(-\cos \frac{\pi }{3}\) = \(\cos \left (\pi – \frac{\pi }{3} \right )\) = \(\cos \frac{2\pi }{3}\)
\(2x = 2n\pi \pm \frac{2\pi }{3}\), where n \(\in\) Z
\(x = n\pi \pm \frac{\pi }{3}\), where n \(\in\) Z
Therefore, the general solution is \(\frac{n\pi }{3}\) or \(n\pi \pm \frac{\pi }{3}\), where n \(\in\) Z.
Miscellaneous Exercise
Q.1: Prove that:
\(2\cos \frac{\pi }{13}\; \cos \frac{9\pi }{13}\; + \cos \frac{3\pi }{13}\; + \cos \frac{5\pi }{13} = 0\)
Sol:
Taking L.H.S.
\(2\cos \frac{\pi }{13}\; \cos \frac{9\pi }{13}\; + \cos \frac{3\pi }{13}\; + \cos \frac{5\pi }{13}\\\) :
= \(\\2\cos \frac{\pi }{13}\; \cos \frac{9\pi }{13}\; + 2\cos \left (\frac{\frac{3\pi }{13} + \frac{5\pi }{13}}{2} \right )\; \cos \left (\frac{\frac{3\pi }{13} – \frac{5\pi }{13}}{2} \right )\\\)
Since, \(\\\boldsymbol{\left [\cos x + \cos y = 2\cos \left ( \frac{x + y}{2} \right )\cos \left ( \frac{x – y}{2} \right ) \right ]}\\\)
= \(\\2\cos \frac{\pi }{13}\; \cos \frac{9\pi }{13}\; + 2\cos \frac{4\pi }{13} \; \cos \left (\frac{-\pi }{13} \right )\\\)
= \(\\2\cos \frac{\pi }{13}\; \cos \frac{9\pi }{13}\; + 2\cos \frac{4\pi }{13} \; \cos \frac{\pi }{13}\\\)
= \(\\2\cos \frac{\pi }{13}\; \left [\cos \frac{9\pi }{13}\; + \cos \frac{4\pi }{13} \right ]\\\)
= \(\\2\cos \frac{\pi }{13}\; \left [2\cos \left ( \frac{\frac{9\pi }{13} + \frac{4\pi }{13}}{2} \right )\; \cos \left ( \frac{\frac{9\pi }{13} – \frac{4\pi }{13}}{2} \right ) \right ]\\\)
= \(\\2\cos \frac{\pi }{13}\; \left [ 2\cos \frac{\pi }{2} \; \cos \frac{5\pi }{26}\right ]\\\)
= \(\\2\cos \frac{\pi }{13} \times 2 \times 0 \times \cos \frac{5\pi }{26}\)
= 0
= R.H.S.
Therefore, \(\boldsymbol{2\cos \frac{\pi }{13}\; \cos \frac{9\pi }{13}\; + \cos \frac{3\pi }{13}\; + \cos \frac{5\pi }{13} = 0}\)
Q.2: Prove that:
\(\left ( \sin 3x + \sin x \right )\sin x + \left ( \cos 3x – \cos x \right )\cos x = 0\)
Sol:
Taking L.H.S.
\(\\\left ( \sin 3x + \sin x \right )\sin x + \left ( \cos 3x – \cos x \right )\cos x\\\) :
= \(\\\sin 3x\; \sin x + \sin ^{2}x + \cos 3x \;\cos x – \cos ^{2}x\\\)
= \(\\\cos 3x \;\cos x + \sin 3x\; \sin x – \left (\cos ^{2}x – \sin ^{2}x \right )\\\)
= \(\\\cos \left ( 3x – x \right ) – \cos 2x\\\)
Since, \(\\\boldsymbol{\left [ \cos \left ( A -B \right ) = \cos A\; \cos B + \sin A \; \sin B \right ]}\\\)
= \(\\\cos 2x – \cos 2x\)
= 0
= R.H.S.
Therefore, \(\boldsymbol{\left ( \sin 3x + \sin x \right )\sin x + \left ( \cos 3x – \cos x \right )\cos x = 0}\)
Q-3: Prove that:
\(\left (\cos x + \cos y \right )^{2} + \left ( \sin x – \sin y \right )^{2} = 4\cos ^{2}\frac{x + y}{2}\)
Sol:
Taking L.H.S.
\(\left (\cos x + \cos y \right )^{2} + \left ( \sin x – \sin y \right )^{2}\\\) :
= \(\\\cos ^{2}x + \cos ^{2}y + 2\cos x\; \cos y + \sin ^{2}x + \sin ^{2}y – 2\sin x\; \sin y\\\)
= \(\\\left (\cos ^{2}x + \sin ^{2}x \right ) + \left (\cos ^{2}y + \sin ^{2}y \right ) + 2 \left (\cos x\; \cos y – \sin x\; \sin y \right )\\\)
= \(\\1 + 1 + 2\cos \left ( x +y \right )\\\)
Since, \(\\\boldsymbol{\left [ \cos \left ( A + B \right ) = \cos A\; \cos B – \sin A \; \sin B \right]}\\\)
= \(\\2 + 2\cos \left ( x +y \right )\\\)
= \(\\2\left [1 + \cos \left ( x +y \right ) \right ]\\\)
= \(\\2\left [1 + 2\cos ^{2}\left ( \frac{x + y }{2}\right ) – 1 \right ]\\\)
Since, \(\\\boldsymbol{\left [\cos 2A = 2\cos ^{2}A – 1 \right ]}\\\)
= \(\\4\cos ^{2}\left ( \frac{x + y}{2} \right )\\\)
= R.H.S.
Therefore, \(\boldsymbol{\left (\cos x + \cos y \right )^{2} + \left ( \sin x – \sin y \right )^{2} = 4\cos ^{2}\frac{x + y}{2}}\)
Q-4: Prove that:
\(\left ( \cos x – \cos y \right )^{2} + \left ( \sin x – \sin y \right )^{2} = 4\sin ^{2}\frac{x – y}{2}\)
Sol:
Taking L.H.S.
\(\left ( \cos x – \cos y \right )^{2} + \left ( \sin x – \sin y \right )^{2}\\\) :
= \(\\\cos ^{2}x + \cos ^{2}y – 2\cos x \; \cos y + \sin ^{2}x + \sin ^{2}y – 2\sin x\; \sin y\\\)
= \(\\\left (\cos ^{2}x + \sin ^{2}x \right ) + \left (\cos ^{2}y + \sin ^{2}y \right ) – 2 \left (\cos x\; \cos y – \sin x\; \sin y \right )\\\)
= \(\\1 + 1 – 2\left [ \cos \left ( x – y \right ) \right ]\\\)
Since, \(\\\boldsymbol{\left [ \cos \left ( A -B \right ) = \cos A\; \cos B + \sin A \; \sin B \right ]}\\\)
= \(\\2\left [ 1 – \cos \left ( x – y \right ) \right ]\\\)
= \(\\2\left [ 1 – \left \{ 1 – 2 \sin ^{2}\left ( \frac{x – y}{2} \right ) \right \} \right ]\\\)
Since, \(\\\boldsymbol{\left [\cos 2A = 1 – 2\sin ^{2}A \right ]}\\\)
= \(\\4\sin ^{2}\frac{x – y}{2}\)
= R.H.S.
Therefore, \(\boldsymbol{\left ( \cos x – \cos y \right )^{2} + \left ( \sin x – \sin y \right )^{2} = 4\sin ^{2}\frac{x – y}{2}}\)
Q-5: Prove that:
\(\sin x + \sin 3x + \sin 5x + \sin 7x = 4\cos x \; \cos 2x \; \cos 4x\)
Sol:
Taking L.H.S.
\(\sin x + \sin 3x + \sin 5x + \sin 7x\\\) :
= \(\\\left (\sin x + \sin 5x \right ) + \left (\sin 3x + \sin 7x \right )\\\)
= \(\\2 \sin \left ( \frac{x + 5x}{2} \right )\; \cos \left ( \frac{x – 5x}{2} \right ) + 2 \sin \left ( \frac{3x + 7x}{2} \right )\; \cos \left ( \frac{3x + 7x}{2} \right )\\\)
Since, \(\\\boldsymbol{\left [\sin A + \sin B = 2\sin \left ( \frac{A +B}{2} \right ).\cos \left ( \frac{A – B}{2} \right ) \right ]}\\\)
= \(\\2\sin 3x \cos \left ( -2x \right ) + 2\sin 5x \cos \left ( -2x \right )\\\)
= \(\\2\sin 3x \cos 2x + 2\sin 5x \cos 2x\\\)
= \(\\2 \cos 2x \left [ \sin 3x + \sin 5x\right ]\\\)
= \(\\2 \cos 2x \left [2 \sin \left ( \frac{3x + 5x}{2} \right ). \cos \left ( \frac{3x – 5x}{2} \right )\right ]\\\)
= \(\\2 \cos 2x \left [2 \sin 4x. \cos \left ( -x \right )\right ]\\\)
= \(\\4 \cos 2x\; \sin 4x \; \cos x\)
= R.H.S.
Therefore, \(\boldsymbol{\sin x + \sin 3x + \sin 5x + \sin 7x = 4\cos x \; \cos 2x \; \cos 4x}\)
Q-6: Prove that:
\(\frac{\left ( \sin 7x + \sin 5x \right ) + \left ( \sin 9x + \sin 3x \right )}{\left ( \cos 7x + \cos 5x \right ) + \left ( \cos 9x + \cos 3x \right )} = \tan 6x\)
Sol:
Since, \(\boldsymbol{\sin A + \sin B = 2\sin \left ( \frac{A + B}{2} \right ). \cos \left ( \frac{A -B}{2} \right )}\\\)
And, \(\\\boldsymbol{\cos A + \cos B = 2\cos \left ( \frac{A + B}{2} \right ). \cos \left ( \frac{A -B}{2} \right )}\)
Taking L.H.S.
\(\\\frac{\left ( \sin 7x + \sin 5x \right ) + \left ( \sin 9x + \sin 3x \right )}{\left ( \cos 7x + \cos 5x \right ) + \left ( \cos 9x + \cos 3x \right )}\\\) :
= \(\\\frac{\left [2\sin \left ( \frac{7x + 5x}{2} \right ). \cos \left ( \frac{7x – 5x}{2} \right ) \right ] + \left [ 2 \sin \left ( \frac{9x + 3x}{2}\right ). \cos \left ( \frac{9x – 3x}{2}\right ) \right ]}{\left [2\cos \left ( \frac{7x + 5x}{2} \right ). \cos \left ( \frac{7x – 5x}{2} \right ) \right ] + \left [ 2 \cos \left ( \frac{9x + 3x}{2}\right ). \cos \left ( \frac{9x – 3x}{2}\right ) \right ]}\\\)
= \(\\\frac{\left [2\sin 6x. \cos x \right ] + \left [ 2 \sin 6x.\cos 3x \right ]}{\left [2\cos 6x.\cos x \right ] + \left [ 2\cos 6x. \cos 3x \right ]}\\\)
= \(\\\frac{2\sin 6x \left [\cos x + \cos 3x \right ]}{2\cos 6x \left [\cos x + \cos 3x \right ] }\\\)
= \(\tan 6x\)
= R.H.S.
Therefore, \(\boldsymbol{\frac{\left ( \sin 7x + \sin 5x \right ) + \left ( \sin 9x + \sin 3x \right )}{\left ( \cos 7x + \cos 5x \right ) + \left ( \cos 9x + \cos 3x \right )} = \tan 6x}\)
Q-7: Show that: \(\sin 3y + \sin 2y – \sin y = 4\sin y \cos\frac{y}{2} \cos\frac{3y}{2}\)
Sol:
Here, L.H.S = \(\sin 3y + \sin 2y\; – \sin y\\\)
= \(\;\\\sin 3y + (\sin 2y \;- \sin y) = \sin 3y + \left [ 2\cos\left ( \frac{2y + y}{2} \right ) \sin\left ( \frac{2y – y}{2} \right ) \right ]\\\)
Since, \(\boldsymbol{(\sin x – \sin y) = \left [ 2\cos\left ( \frac{x + y}{2} \right ) \sin\left ( \frac{x – y}{2} \right ) \right ]}\)
= \(\\\sin 3y + \left [ 2\cos\left ( \frac{3y}{2} \right ) \sin\left ( \frac{y}{2} \right ) \right ]\\\)
=\( \left [ 2\sin\left ( \frac{3y}{2} \right ) \cos\left ( \frac{3y}{2} \right ) \right ] + \left [ 2\cos\left ( \frac{3y}{2} \right ) \sin\left ( \frac{y}{2} \right ) \right ]\\\)
Since, sin 2x = 2 sin x cos x
=\(\\2\cos\frac{3y}{2}\cdot [ \sin\ \frac{3y}{2} + \sin \frac{y}{2}]\\\)
=\(2\cos\frac{3y}{2}\cdot [ \sin\ \frac{(\frac{3y}{2} + \frac{y}{2})}{2}][ \cos\ \frac{(\frac{3y}{2} – \frac{y}{2})}{2}]\)
Since, sin x + sin y = \(\boldsymbol{\\2\sin\left ( \frac{x + y}{2} \right )\cos\left ( \frac{x – y}{2} \right )}\)
\(\\= 2\cos\left ( \frac{3y}{2} \right )2\sin y \cos\left ( \frac{y}{2} \right )\) \(\\= 4\sin y\cos\left ( \frac{y}{2} \right ) \cos\left ( \frac{3y}{2} \right )\)
= R.H.S
Q-8: The value of \(\tan y = -\frac{4}{3}\) where y in in 2nd quadrant then find out the values of \(\sin \frac{y}{2}, \cos \frac{y}{2} \;and\; \tan\frac{y}{2}\).
Sol:
Here, y is in 2nd quadrant.
So, \(\frac{\pi}{2} < y < \pi \\ \\ \Rightarrow \frac{\pi}{4} < \frac{y}{2} < \frac{\pi}{2}\)
Thus, \(\sin \frac{y}{2}, \cos \frac{y}{2} \;and\; \tan\frac{y}{2}\) lies in 1st quadrant.
Now,
\(\tan y = -\frac{4}{3}\) \(\sec^{2} y = 1 + \tan^{2} y = 1 + (\frac{4}{3})^{2} = 1 + \frac{16}{9} = \frac{25}{9}\\\)
So, \(\cos^{2} y = \frac{9}{25}\)
\(\Rightarrow \cos y = \pm \frac{3}{5}\)
As y is in 2nd quadrant, cos y is negative.
\(\cos y = \frac{-3}{5}\)
So, cos y = \(2\cos^{2} \frac{y}{2} – 1\)
\(\Rightarrow \frac{-3}{5} = 2\cos^{2} \frac{y}{2} – 1 \\ \\ \Rightarrow 2\cos^{2} \frac{y}{2} = 1 – \frac{-3}{5} \\ \\ \Rightarrow 2\cos^{2} \frac{y}{2} = \frac{2}{5} \\ \\ \Rightarrow 2\cos^{2} \frac{y}{2} = \frac{1}{5} \\ \\ \Rightarrow 2\cos^{2} \frac{y}{2} = \frac{3}{\sqrt{5}}\) [Since, \(\boldsymbol{\cos\frac{y}{2}}\) is positive]
\(\Rightarrow \cos\frac{y}{2} = \frac{\sqrt{5}}{5} \\ \\ \sin^{2} \frac{y}{2} + \cos^{2} \frac{y}{2} = 1 \\ \\ \Rightarrow \sin^{2} \frac{y}{2} + \cos^{2} \frac{1}{\sqrt{5}} = 1 \\ \\ \Rightarrow \sin^{2} \frac{y}{2} = 1 – \frac{1}{5} = \frac{4}{5} \\ \\ \Rightarrow \sin^{2} \frac{y}{2} = \frac{2}{\sqrt{5}}\) [Since, \(\boldsymbol{\sin\frac{y}{2}}\) is positive]
\(\Rightarrow \sin^{2} \frac{y}{2} = \frac{2\sqrt{5}}{5} \\ \\ \tan \frac{y}{2} = \frac{\sin\frac{y}{2}}{\cos\frac{y}{2}} = \frac{\frac{2}{\sqrt{5}}}{\frac{1}{\sqrt{5}}} = 2\)
Q-9: The value of \(\cos y = -\frac{1}{3}\) where y in in 3rd quadrant then find out the values of \(\sin \frac{y}{2}, \cos \frac{y}{2} \;and\; \tan\frac{y}{2}\).
Sol:
Here, y is in 3rd quadrant.
So, \(\pi < y < \frac{3\pi}{2} \\ \\ \Rightarrow \frac{\pi}{2} < \frac{y}{2} < \frac{3\pi}{4}\)
Thus, \(\cos \frac{y}{2} \;and\; \tan\frac{y}{2}\) are negative and \(\sin \frac{y}{2}\) is positive.
Now, \(\cos y = -\frac{1}{3}\) [Given]
\(\cos y = 1 – 2\sin^{2}\frac{y}{2} \Rightarrow \sin^{2}\frac{y}{2} = \frac{1 – \cos y}{2} \Rightarrow \sin^{2}\frac{y}{2} = \frac{1 – \frac{-1}{3}}{2} = \frac{1 + \frac{1}{3}}{2} = \frac{2}{3}\\\)
\(\\\Rightarrow \boldsymbol{\sin \frac{y}{2}} = \frac{\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{6}}{3}\\\) [Since, \(\sin\frac{y}{2}\) is positive]
Now, \(\cos y = 2\cos^{2}\frac{y}{2} – 1\)
\(2\cos^{2}\frac{y}{2} = \frac{1 + \cos y}{2} = \frac{1 – \frac{1}{3}}{2} = \frac{1}{3}\\\)
\(\\\Rightarrow\) \(\boldsymbol{\cos \frac{y}{2}}= \frac{-1}{\sqrt{3}} = \frac{-1}{\sqrt{3}}\times \frac{-\sqrt{3}}{3} = \frac{-1}{\sqrt{3}}\)
Therefore, \(\boldsymbol{\tan\frac{y}{2}} = \frac{\sin\frac{y}{2}}{\cos\frac{y}{2}} = \frac{\frac{\sqrt{2}}{\sqrt{3}}}{\frac{-1}{\sqrt{3}}} = -\sqrt{2}\)
Q-10: The value of \(\sin y = \frac{1}{4}\) where y in in 2nd quadrant then find out the values of \(\sin \frac{y}{2}, \cos \frac{y}{2} \;and\; \tan\frac{y}{2}\).
Sol:
Here, y is in 2nd quadrant.
So, \(\frac{\pi}{2} < y < \pi \\ \\ \Rightarrow \frac{\pi}{4} < \frac{y}{2} < \frac{\pi}{2}\)
Thus, \(\sin \frac{y}{2}, \cos \frac{y}{2} \;and\; \tan\frac{y}{2}\) lies in 1st quadrant.
Now, \(\sin y = \frac{1}{4}\)
\(\\\cos^{2} y = 1 – 2\sin^{2} y = 1 – (\frac{1}{4})^{2} = 1 – \frac{1}{16} = \frac{15}{16} \\ \\ \Rightarrow \cos y = -\frac{\sqrt{15}}{4}\) [Since, \(\cos y\) is negative]
\(\sin^{2} \frac{y}{2} = \frac{1 – (\frac{-\sqrt{15}}{4})}{2} = \frac{4 + \sqrt{15}}{8}\\\)
\(\\\Rightarrow \) \(\boldsymbol{\sin \frac{y}{2}} = \sqrt{\frac{4 + \sqrt{15}}{8}}\) [ Since, \(\sin\frac{y}{2}\\\) is positive ]
=\(\\\sqrt{\frac{4 + \sqrt{15}}{8}\times \frac{2}{2}}= \sqrt{\frac{8 + 2\sqrt{15}}{16}} =\boldsymbol{\frac{\sqrt{8 + 2\sqrt{15}}}{4}}\\\)
\(\\\cos^{2} y = \frac{1 + \cos y}{2} = \frac{1 + (-\frac{\sqrt{15}}{4})}{2} = \frac{4 – \sqrt{15}}{8}\\\)
Therefore, \(\boldsymbol{\cos \frac{y}{2}}= \sqrt{\frac{4 – \sqrt{15}}{8}}\) = \(\sqrt{\frac{4 – \sqrt{15}}{8}\times \frac{2}{2}}\\\)
= \(\sqrt{\frac{8 – 2\sqrt{15}}{16}}=\boldsymbol{\frac{\sqrt{8 – 2\sqrt{15}}}{4}}\)
Now, \(\boldsymbol{tan \frac{y}{2}} = \frac{\sin \frac{y}{2}}{\cos \frac{y}{2}} = \frac{\left ( \frac{\sqrt {8\; + \;2\sqrt{15}}}{4} \right )}{\left ( \frac{\sqrt {8\; -\; 2\sqrt{15}}}{4} \right )}\)
= \(\\\frac{\sqrt{8 + 2\sqrt{15}}}{\sqrt{8 – 2\sqrt{15}}} = \frac{\sqrt{8 + 2\sqrt{15}}}{\sqrt{8 – 2\sqrt{15}}}\times \frac{\sqrt{8 + 2\sqrt{15}}}{\sqrt{8 + 2\sqrt{15}}}\\\\\)
= \(\\\frac{\sqrt{(8 + 2\sqrt{15})^{2}}}{\sqrt{64\; -\; 60}} = \frac{8 + 2\sqrt{15}}{2} =\boldsymbol{4 + \sqrt{15}}\)