Simple Harmonic Motion: Circle of Reference
The oscillations of a harmonic oscillator can be represented by terms containing sine and cosine of an angle. If the displacement of an oscillatory particle from its mean position can be represented by an equation
y = a sinθ or y = a cosθ or y = A sinθ + B cosθ,
where a, A and B are constants, the particle executes simple harmonic motion.
A particle is said to execute simple harmonic motion if it moves to and fro about a fixed point periodically, under the action of a force F which is directly proportional to its displacement x from the fixed point and the direction of the force is opposite to that of the displacement.
Mathematically,
F = – kx
where k is constant of proportionality.
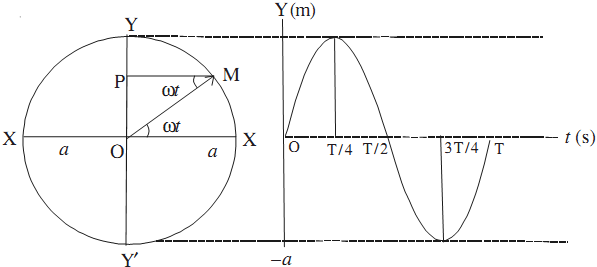
To derive the equation of simple harmonic motion, consider a point M moving with a constant speed v in a circle of radius a with centre O. At t = 0, let the point be at X. The position vector OM specifies the position of the moving point at time t.
The position vector OM, also called the phaser, rotates with a constant angular velocity ω = v/a. The acceleration of the point M is v2/a = aω2 towards the centre O.
At time t, the component of this acceleration along OY = aω2 sin ωt. Draw MP perpendicular to YOY′. Then P can be regarded as a particle of mass m moving with an acceleration aω2 sin ωt. The force on the particle P towards O is given by
F = maω2 sin ωt
But sin ωt = y/a. Therefore
F = mω2y
The displacement is measured from O towards P and force is directed towards O. Therefore,
F = – mω2y
Since this force is directed towards O, and is proportional to displacement ‘y’ of P from O, the particle P is executing simple harmonic motion.
Let mω2 = k, a constant.
F = – ky
The constant k, which is force per unit displacement, is called force constant. The angular frequency of oscillations is given by
ω2 = k/m
In one complete rotation, OM describes an angle 2π and it takes time T to complete one rotation. Hence
ω = 2π/T
T = 2π/km
This is the time taken by P to move from O to Y, then through O to Y′ and back to O.During this time, the particle moves once on the circle and the foot of perpendicular from its position is said to make an oscillation about O.