Static and Kinetic Friction
Consider a block resting on some horizontal surface. Let some external force Fext be applied on the block. Initially the block does not move. This is possible only if some other force is acting on the block. The force is called the force of static friction and is represented by fs.
As Fext is increased, fs also increases and remains equal to Fext in magnitude until it reaches a critical value fs(max). When Fext is increased further, the block starts to slide and is then subject to kinetic friction.
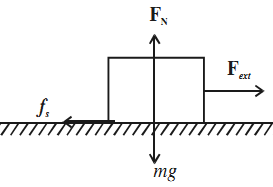
It is common experience that the force needed to set an object in motion is larger than the force needed to keep it moving at constant velocity. For this reason, the maximum value of static friction fs between a pair of surfaces in contact will be larger than the force of kinetic friction fk between them.
Static Friction
fs(max) ∝ FN
fs(max) = µs FN
where µs is called the coefficient of static friction. The normal force FN of the surface on the block can be found by knowing the force with which the block presses the surface.
Since fs = Fext for fs ≤ fs(max)
fs ≤ µs FN
Kinetic Friction
fk = µk FN
where µk is the coefficient of kinetic friction.
In general, µs > µk
Values of µs and µk for a given pair of materials depend on the roughness of surfaces, cleanliness, temperature, humidity, etc.